В этом руководстве вы узнаете,
как устроены тесты на числовые последовательности, какие типы числовых
последовательностей существуют и как проходить такие тесты.
В конце руководства будет ссылка на бесплатный тренировочный тест из 20 вопросов, пройдя который вы оцените свой уровень
подготовки.
Время чтения - 6 минут
Быстрый переход по разделам
Кратко: что такое тест на числовые последовательности?
Какие есть типы числовых последовательностей?
Типы заданий теста на числовые последовательности
Арифметическая + геометрическая прогрессии
Как решать тесты на числовые последовательности?
Пройти бесплатный пробный тест
Кратко: что такое тест на числовые
последовательности?
Тест на числовые последовательности – это особый тип теста для оценки числовых и логических способностей кандидата. В таком тесте вам даются различные числовые последовательности, для которых необходимо определить следующий элемент (элементы) или пропущенный элемент.
Пример теста на числовые последовательности из базы тестов test-help.com:
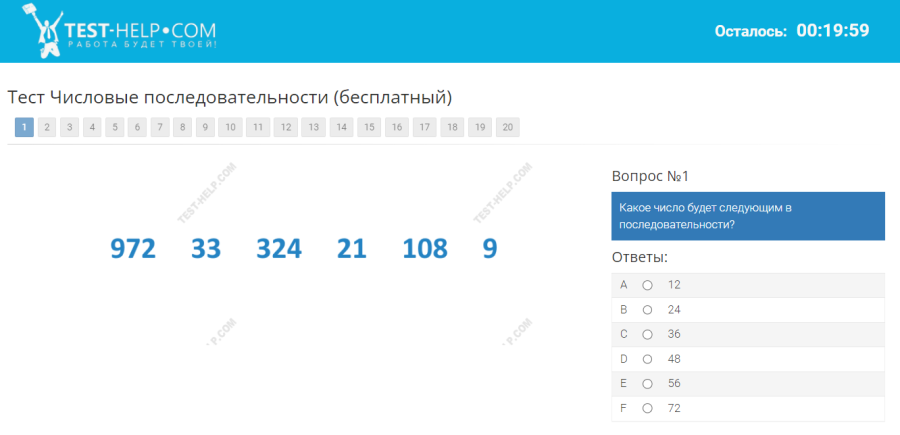
Числовая последовательность – это ряд чисел (элементов),
объединенных определенной функцией/функциями.
Функция – арифметическое действие или комплекс арифметических
действий (сложение, вычитание, умножение, деление).
Элемент - каждое число в последовательности.
Номер элемента – порядковый номер элемента в числовой
последовательности, например, в последовательности 5, 10, 15, 20, 25, 30 число
15 будет третьим элементом последовательности.
Аргумент – независимая величина (число), которое применяется при вычислении функции.
Какие есть типы
числовых последовательностей?
Рассмотрим два основных типа числовых последовательностей:
Арифметическая
прогрессия
В арифметической прогрессии каждый следующий элемент больше
предыдущего элемента на определенное число (аргумент) – в приведенном примере это
число 2. Данная последовательность является возрастающей.
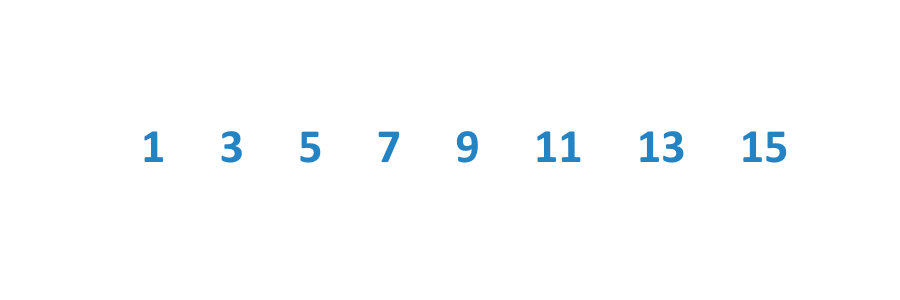
Разновидностью данного типа является последовательность, где аргументом
является число с отрицательным значением. В таком случае последовательность
будет убывающей. Приведем пример:
.png)
В данной последовательности каждый последующий элемент образуется путем вычитания 25 от предыдущего.
Геометрическая
прогрессия
В геометрической прогрессии каждый следующий элемент, начиная со второго, образуется умножением предыдущего элемента на определенное число – в приведённом примере это число 3.

Разновидностью данного типа является последовательность, где аргумент
не множитель, а делитель. В таком случае последовательность будет убывающей.
Приведем пример:
.png)
В данной последовательности каждый последующий элемент
образуется путем деления на 2 предыдущего элемента.
Итак, мы рассмотрели два основных типа и два подтипа числовых последовательностей для того, чтобы вы понимали, как они образуются. На практике же, тестирующие компании составляют различные вариации последовательностей, например, применяя два типа в одной последовательности. Ниже мы рассмотрим наиболее распространенные типы заданий тестов на числовые последовательности. Каждому такому типу мы присвоили неофициальное рабочее название для большей запоминаемости.
Типы
заданий теста на числовые последовательности
Сумма двух
предыдущих чисел
Этот тип последовательности составляется по принципу чисел
Фибоначчи, где первые два элемента последовательности - это две единицы, а
каждый последующий элемент является суммой двух предыдущих элементов (1, 1, 2,
3, 5, 8, 13, 21 и так далее). Отличие от чисел Фибоначчи лишь в том, что первые
два элемента последовательности – произвольные числа.

При анализе видим, что эта последовательности возрастающая, первые два элемента этой последовательности – 12 и 23. Третий элемент образуется путем сложения первых двух: 12+23 = 35. Четвертый элемент образуется путем сложения второго и третьего элементов: 23+35 = 58 и т.д.
Прибавление/убавление
Этот тип последовательности составляется путем использования
2 аргументов, которые применяются попеременно. Приведем пример.

При анализе этой последовательности видим, что она не
является убывающей или возрастающей – назовем ее смешанной. Второй элемент
последовательности больше первого на 5 (125+5 = 130), третий элемент меньше
второго на 15 (130-15 = 115), четвертый больше третьего на 5 (115+5 = 120),
пятый меньше четвертого на 15 (120-15 = 105) и тд. Мы видим, что в этой
последовательности попеременно применяются 2 аргумента +5 и -15.
Разновидности данного типа последовательности:
- оба аргумента являются положительными числами (последовательность в этом случае будет возрастающей, функция прибавления к элементам в таком случае может выглядеть, например, так: +5 +10 +5 +10 и т. д);
- оба аргумента являются отрицательными числами (последовательность в этом случае будет убывающей, функция вычитания от элементов в таком случае может выглядеть, например, так: -3 -12 -3 -12 и т. д).
Прибавление/убавление (2 в 1)
Данная последовательность является вариацией предыдущего типа
последовательности, с той лишь разницей, что в этом типе последовательности два
первых элемента – произвольные числа и аргументы применяются к соответствующим
элементам. Данная последовательность состоит из двух независимых последовательностей.
Первая последовательность идет по нечетным элементам (нечетная
последовательность) – 1, 3, 5 и т. д, вторая последовательность по четным
элементам (четная последовательность) – 2, 4, 6 и т. д.
.png)
Анализируя данную последовательность видим, что она смешанная
(не возрастает и не убывает). Далее находим зависимость по элементам нечетной последовательности
(элементы 1, 3, 5). Это числа 150, 160, 170 – каждый последующий элемент нечетной
последовательности получается прибавлением 10 к предыдущему элементу.
Зависимость по элементам четной последовательности (элементы 2, 4, 6) – числа 240,
220, 200. Каждый последующий элемент нечетной последовательности получается
вычитанием 20 от предыдущего элемента.
Разновидности данного типа последовательности:
- оба аргумента являются
положительными числами;
- оба аргумента являются отрицательными числами.
Арифметическая + геометрическая прогрессии
Данная последовательность содержит в себе две
последовательности – по нечетным и четным числам. Одна из последовательностей –
арифметическая, другая геометрическая. Приведем пример.

Анализируя данную последовательность видим, что она смешанная
(не возрастает и не убывает). Далее находим зависимость по элементам нечетной последовательности
(элементы 1, 3, 5). Это числа 800, 400, 200 – каждый последующий элемент нечетной
последовательности получается делением на 2 предыдущего элемента. Зависимость
по элементам четной последовательности (элементы 2, 4, 6) – числа 600, 550, 500.
Каждый последующий элемент нечетной последовательности получается вычитанием 50
от предыдущего элемента.
Разновидности данного типа последовательности:
- один аргумент отрицательное число
(вычитание), второй – множитель;
- один аргумент положительное число
(прибавление), второй – множитель;
- один аргумент положительное число (прибавление), второй – делитель.
Кратное
прибавление
Каждый элемент данной последовательности образуется путем сложения
предыдущего элемента с разностью между двумя предыдущими элементами последовательности,
умноженной на постоянный множитель. Первые два элемента последовательности –
произвольные числа.

Анализируя данную последовательность видим, что она
возрастающая.
Третий элемент последовательности образуется путем сложения
второго элемента и разности между вторым и первым, умноженным на два
(50+(50-10)*2 = 130. Аналогично образуется четвертый элемент последовательности: 130+(130-50)*2 = 290.
Разновидности данного типа последовательности:
- элемент 1 больше, чем элемент 2, в таком случае последовательность будет убывающей.
Случайные
числа
Данный тип последовательности может очень усложнить решение
задачи. В такой последовательности, например, нечетная последовательность (элементы
1, 3, 5 и т. д) представляет собой арифметическую или геометрическую
последовательность, а четная последовательность (элементы 2, 4, 6 и т. д)
представляет собой набор случайных чисел. Приведем пример.

Анализируя данную последовательность видим, что она смешанная (не возрастает и не убывает). Далее находим зависимость по элементам нечетной последовательности (элементы 1, 3, 5). Это числа 20, 100, 500 – каждый последующий элемент нечетной последовательности получается умножением на 5 предыдущего элемента. Зависимость по элементам четной последовательности (элементы 2, 4, 6) – числа 286, 509, 731. Каждый последующий элемент четной последовательности нельзя вычислить какой-либо функцией, он является случайным числом.
Как решать
тесты на числовые последовательности?
Ниже приведем рекомендуемый алгоритм решения тестов на числовые последовательности.
1. Внимательно
посмотрите на последовательность, определите ее тип – возрастающая, убывающая
или смешанная.
2. Если последовательность возрастающая, скорее всего вы имеете дело с арифметической или геометрической прогрессией, где каждый новый элемент больше предыдущего на определенное значение или на определенный множитель.
3. Если последовательность убывающая, вероятно, вы также имеете дело с подтипами арифметической или геометрической прогрессий, где каждый новый элемент меньше предыдущего на определенное значение или на определенный делитель.
4. Если последовательность смешанная, ищите сначала зависимость от первого элемента (например, +10 -20 +10 -20 или *3 /4 *3 /4 и т. д). Если такой зависимости не наблюдается, ищите зависимости по нечетной (элементы 1, 3, 5 и т. д) и четной (элементы 2, 4, 6 и т. д) последовательностям.
Чем больше вы будете
практиковаться, тем лучше будете видеть зависимости в таких тестах.
Пройти бесплатный пробный тест на числовые последовательности можно здесь.
Помните правило “4П” – “Провалить подготовку – подготовить провал”.
Удачи вам на тестировании!
